Quantificare l’incertezza di misura
Con questo articolo si riporta il significato di incertezza di misura e come quantificarla nell’attività di un laboratorio di analisi chimiche.
Quantificare l’incertezza di misura
Il concetto di incertezza di misura non è nuovo, anzi è noto da molto tempo (Stephen M. Stigler, The history of statistics: the measurement of uncertainty before 1900. Harvard University Press).
Le regole per la valutazione dell’incertezza sono state riportate nella “Guide to the expression of Uncertainty in Measurement” (GUM) da parte dell’ISO [8] e tradotta in italiano col documento UNI CEI ENV 13005:2000 [9].
Le difficoltà di applicare il concetto di incertezza alla chimica analitica, come definito dalla GUM, ha indotto Eurachem a produrre una guida “Quantifying Uncertainty in Analytical Measurement” per la sua applicazione nelle misurazioni chimiche .
La seconda edizione di tale linea guida EURACHEM è stata tradotta in lingua italiana dall’Istituto Superiore di Sanità (ISS).
Nella linea guida si riporta il concetto d’incertezza distinto da quello di errore; segue una descrizione per la valutazione dell’incertezza di misura.
Documenti
In data 14 ottobre 2015 la linea guida UNI CEI ENV 13005:2000 è stata ritirata da UNI.
Il 15 dicembre 2015, la Commissione Tecnica “Metrologia” (organo tecnico misto UNI/CEI), ha adottato con traduzione la Guida ISO/IEC 98-3:2008 che rappresenta la riedizione in vigore della GUM:1995 in ambito ISO/IEC [10].
La Guida ISO/IEC 98-3:2008, in lingua inglese, è pubblicata sul sito del BIPM – Bureau International des Poids et Measures come JCGM Guide 100 [1].
Dal mese di settembre 2016 la Guida è diventata norma tecnica nazionale: UNI CEI 70098-3 [10].
Incertezza di misura: definizione
Nel documento JCGM Guide 100 [1], [12], punto 2.2.3, si trova la definizione di incertezza di misura:
“parametro associato al risultato di una misura, che caratterizza la dispersione dei valori che potrebbe ragionevolmente essere attribuito al misurando“.
Precisione e Giustezza: definizione
Nella definizione di incertezza riscontriamo due concetti:
- dispersione dei valori: richiama il concetto di precisione
- attribuito al misurando: fa riferimento alla giustezza
La precisione di misura viene definita nel VIM al punto 2.15, a cui si rimanda (vedi sito internet). La definizione di precisione è ancor più dettagliata con note dedicate a cui si rimanda.
Nel punto 2.14 del VIM si definisce la giustezza: “grado di concordanza tra la media di un numero infinito di valori misurati ripetuti e un valore di riferimento”. Nelle note si precisa che la “giustezza varia in modo inverso con l’errore sistematico, ma non ha relazione con l’errore casuale“.
Misure e valor vero
Risultati tra loro differenti
Ogni giorno, in laboratorio vengono prodotti tante misure che, il più delle volte, rappresentano il prodotto che viene presentato al Cliente.
E’ risaputo che eseguendo più volte la stessa misura, in condizioni di ripetibilità, i risultati ottenuti risultano comunque tra loro differenti e si collocano attorno al valore vero. Inoltre, più è piccola la dimensione della regione in cui si dispongono tali risultati, tanto migliore è la qualità della misura condotta.
In altre parole, ogni volta che in laboratorio si effettua una misura si ottiene solo una stima del valore misurato, e la dispersione dei valori ottenuti dalle diverse misure effettuate rappresenta la bontà della stima [11].
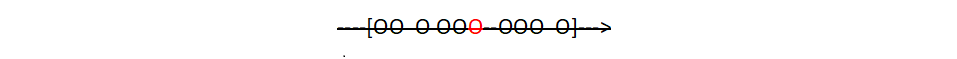
O = risultato della misura; O = con colore rosso indica il valore medio delle misure
Un insieme di valori
Al punto 2.11 del VIM, Nota 1 si legge: “… a causa della quantità intrinsecamente incompleta di dettagli nella definizione di qualsiasi grandezza, non esiste un unico valor vero, bensì un insieme di valori veri, tutti coerenti con la definizione della grandezza“.
Questo insieme di valori è sconosciuto; per conoscerlo servono infinite informazioni. Con un numero finito di informazioni a disposizione, ossia ciò che avviene nella pratica, non si può avere la conoscenza del risultato vero, ma solo un dato incerto [2].
Intervallo di valori
Pertanto, il risultato di una misura non è un solo valore ma un intervallo finito, con ampiezza variabile, in funzione delle informazioni disponibili, comprese le condizioni in cui sono state effettuate le misure [2], che contiene il valore vero, comunque sconosciuto sconosciuto.
Tutti i valori compresi nell’intervallo sono equivalenti tra loro ed indistinguibili uno dall’altro.
La parola incertezza significa dubbio, e pertanto l’incertezza di misura, nella sua accezione più ampia, significa dubbio circa la validità del risultato della misura [3], [12].
Nella realtà ed al contrario di quello che verrebbe da pensare, la conoscenza dell’incertezza implica un aumento della significatività e della validità delle informazioni circa il risultato della prova[13].
Errore di misura
Obiettivo
L’obiettivo di una qualsiasi misura è quello di determinare il valore del misurando.
In primo luogo, si definisce il misurando oggetto di interesse mentre, in secondo luogo, con la sequenza logica delle operazioni riportate nel metodo di prova (o di misura) ed eseguite con cura dagli operatori del laboratorio si consegue la misura.
Anche la procedura adottata, dalla quale si ottiene la misura, deve dettagliare le azioni per consentire a un Tecnico di Laboratorio abilitato all’esecuzione della prova, di eseguire la misura certo di disporre di tutte le informazioni [1], [12].
Risultato della misura
Il risultato di una misura, spesso ottenuto da una serie di osservazioni in condizione di ripetibilità, è solo un’approssimazione del valore del misurando [1], [12].
Per far fronte alla carenza di informazioni che gravano sul risultato finale, il risultato è accompagnato dal valore di incertezza.
E’ risaputo che l’errore nella misura di una grandezza si ottiene dalla differenza tra il valore misurato ed il riferimento. Per una singola misura su un campione di prova, non è possibile conoscere l’errore, poiché, in questo caso, il valore di riferimento (della grandezza) è il valore vero del misurando, che non è noto [1].
Errore casuale e sistematico
Nel dettaglio, l’errore di una misura è costituito da una componente sistematica e da una casuale che, in altre parole rappresentano le variazioni, prevedibili e non, in una serie di misure ottenute in condizioni di ripetibilità [1], [12].
Errore casuale
L’errore casuale deriva da variazioni non prevedibili i cui effetti originano differenze nelle misure del misurando, ottenute in condizioni di ripetibilità. L’errore casuale non si può eliminare, ma si può ridurre al crescere del numero delle misure.
Il valore esatto dell’errore nella media derivante dagli effetti casuali non può essere conosciuto [1], [12]. Lo scarto tipo di una serie di misure rappresenta il contributo all’incertezza dovuta agli effetti casuali.
Errore sistematico
L’errore sistematico è la componente dell’errore che resta costante in presenza di misurazioni ripetute o varia in maniera prevedibile [1].
L’errore sistematico non può essere eliminato, ma può essere ridotto. Se l’errore sistematico è determinato da un effetto noto sul risultato di una misura (scostamento o bias), può essere quantificato.
Se tale errore è significativo rispetto alle specifiche di accuratezza della misura, si può compensare l’effetto applicando un fattore di correzione attraverso il quale il valore atteso dell’errore sistematico dovrebbe annullarsi.
Il valore di bias rappresenta il contributo all’incertezza della misura dovuto all’errore sistematico [1].
La combinazione matematica dei contributi dovuti all’errore casuale ed a quello sistematico è una delle modalità per valutare l’incertezza composta di una misura.
L’incertezza di tipo composta può essere valutata in varie modalità che andremo a dettagliare in uno specifico articolo.
Espressione del risultato
Assumendo una distribuzione normale dei risultati delle misure, la miglior stima del valore vero è espresso tramite la media dei risultati delle misure effettuate.
Per rendere confrontabile il risultato di un analisi, con un valore di riferimento o con il risultato conseguito da un altro laboratorio, lo si accompagna con parametro che quantifica la dispersione dei risultati delle misure condotte per stimare il valore vero.
Perciò il:
misurando = risultato ± range
Indicando con y il risultato ed U il range abbiamo:
misurando = y ± U
dove con la lettera U si indica il valore dell’incertezza estesa.
Incertezza estesa U
Considerando che U deriva dal prodotto dell’incertezza composta uc per il fattore di copertura K:
U = k * uc
e il :
misurando = y ± k * uc
Il valore del fattore di copertura k viene scelto sulla base del livello di confidenza richiesto per l’intervallo y – U a y + U.
Il fattore di copertura è pari a:
- k = 2 con livello di confidenza del 95%
- K =3 per un livello di confidenza del 99 %.
In altre parole, l’incertezza del risultato di una misura evidenzia l’indeterminazione del valore del misurando.
Il risultato di una misura ottenuta è ancora solo una stima del valore del misurando a causa dell’incertezza derivante da effetti casuali e sistematici [1], [12].
Esempio di calcolo
- analisi di una sostanza chimica generica: “x” in un prodotto ortofrutticolo, ad esempio una mela
- risultato della misura della concentrazione: y = 0.10 mg/kg
- incertezza estesa U = 0.05 mg/kg
si scrive:
misurando = 0.10 ± 0.05 mg/kg
In altre parole significa che il valore vero del misurando si colloca in un range di valori compresi fra 0.05 e 0.15 mg/kg.
Fonti di incertezza
Le fonti più comuni di incertezza sul risultato della misura di una sostanza chimica sono le seguenti [1], [12]:
- definizione incompleta del misurando
- imperfetta realizzazione della definizione del misurando
- non rappresentatività della campionatura
- condizioni di conservazione inadeguate
- effetti non identificati di condizioni ambientali sulla misura
- imperfetta misura delle condizioni stesse
- inadeguata definizione della stechiometria di una reazione
- purezza dei reagenti
- effetti non identificati di altre sostanze presenti nella matrice
- distorsioni nell’uso o nella lettura di strumenti
- risoluzione strumentale non infinita
- valori non esatti dei materiali di riferimento
- valori non esatti di parametri (es. costanti) utilizzati nei calcoli
- approssimazioni inerenti al metodo di misura
Norme ed incertezza
L’incertezza di misura deve essere valutata perchè prescritta dalla norma (norma UNI EN ISO/IEC 17025:2018). Perciò, un laboratorio che esegue la prova deve identificare e tenere conto dei contributi significativi per valutare l’incertezza di misura e, soprattutto, la deve riportare nel rapporto di prova perchè:
- essa è rilevante per la validità o l’utilizzo dei risultati di prova;
- è richiesta dal cliente;
- influisce sulla conformità rispetto ad un limite di specifica.
Alcune norme
Nei settori ambientali e alimentari, alcune norme di riferimento, tecniche e di legge richiedono di valutare l’incertezza di misura:
- Reg. (UE) 2017/625 del 15.03.2017, relativo ai controlli ufficiali…
- D. Lgs. 10.12.2010, n. 219 Attuazione della direttiva 2008/105/CE relativa a standard di qualità ambientale ….
- Decreto 14.06.2017 Recepimento della direttiva (UE) 2015/1787 che modifica gli allegati II e III della direttiva 98/83/CE …
- SANTE/12682/2019 Analytical quality control and method validation procedures for pesticide residues analysis in food and feed, Implemented by 01/01/2020.
Norme ed obiettivi di qualità
Alcune delle stesse norme riportate prevedono obiettivi di qualità per l’incertezza di misura:
- D. Lgs. 10.12.2010, n. 219: “…l’incertezza estesa associata al risultato di misura non deve essere superiore al 50% del valore dello standard di qualità…”
- Decreto 14.06.2017: Viene precisata la possibilità di avere un’incertezza per diversi pesticidi al 30%. Per altri pesticidi tali valore può arrivare sino a 80%.
- Sante/12682/2019: “… Dai test valutativi dell’UE è stata calcolata una MU espansa predefinita del 50% (corrispondente a un livello di confidenza del 95% e un fattore di copertura di 2).”
A chi serve l’incertezza
La conoscenza dell’incertezza di misura è importante per il :
- Cliente: serve per confrontare il misurando con un valore di specifica (limite di legge)
- Laboratorio: preposto al controllo ufficiale per esprimere il giudizio di conformità ad una norma specifica
Regole decisionali
Nel Manuale e Linee Guida 52/2009 riscontriamo:
- Con le norme di riferimento, tecniche o di Legge, che riportano o indicano le regole decisionali per l’analisi di conformità: queste devono essere utilizzate.
- Allo stesso modo quando gli utenti delle misure, responsabili di eventuali azioni ad esse collegate, definiscono le regole decisionali per l’analisi di conformità: queste devono essere utilizzate.
- In assenza di regole decisionali per l’analisi di conformità si usa un criterio probabilistico.
- Il Risultato della misura R > VL determina la non conformità con probabilità 95%. In altre parole il campione è non conforme al VL quando il risultato della misura supera il VL oltre ogni ragionevole dubbio, cioè tenendo conto dell’incertezza di misura (U), stimata ad un livello di confidenza del 95% .
UNI EN ISO/IEC 17025:2018 e SANTE/12682/2019
In conclusione, la UNI EN ISO/IEC 17025:2018 prevede che il laboratorio documenti ed applichi la regola decisionale utilizzata per la dichiarazione di conformità ad una specifica o ad una norma.
Ad esempio: la regola decisionale riportata nel documento Sante/12682/2019 punto E15. Riguarda il controllo dei residui dei prodotti fitosanitari negli alimenti di origine vegetale:” … la conformità con il limite massimo di residuo (LMR) deve essere verificata. Si assume che il LMR sia superato se il valore misurato supera l’LMR di più dell’incertezza estesa (x – U > MRL).
In questi casi il campione è non conforme.
Norme di riferimento
- UNI CEI EN ISO/IEC 17025:2018, Requisiti generali per la competenza dei laboratori di prova e taratura
- September 2008, JCGM 100:2008 GUM 1995 with minor corrections Evaluation of measurement data — Guide to the expression of uncertainty in measurement
- UNI CEI 70098-3 Incertezza di misura – Parte 3: guida all’espressione dell’incertezza di misura, settembre 2016
Per saperne di più
- ISO, www.iso.org
- UNI, www.store.uni.com
- ACCREDIA, https://www.accredia.it/
- VIM, https://www.ceinorme.it/it/normazione-it/vim/
Bibliografia
[1] September 2008, JCGM 100:2008 GUM 1995 with minor corrections Evaluation of measurement data — Guide to the expression of uncertainty in measurement
[2] Incertezza di misura, D.Argentini, Arpa Lazio, A.Grigato, Arpa Veneto, Il Bollettino, 2011/2-3
[3] Seminario, Dati analitici e valori limite, Incertezza delle misure e certezza del diritto, Palermo 20.10.2010
[4] Comparative Study of the Main Top-down Approaches for the Estimation of Measurement Uncertainty in Multiresidue Analysis of Pesticides in Fruits and Vegetables, Journal of Agricultural and Food Chemistry
[5] Ispra, L’analisi di conformità con i valori di legge: il ruolo dell’incertezza associata a risultati di misura, Manuali e linee guida 52/2009
[6] ISPRA, Rete delle Agenzie Ambientali, L’ANALISI DI CONFORMITA’ CON I VALORI LIMITE DI LEGGE: IL RUOLO DELL’INCERTEZZA ASSOCIATA A RISULTATI DI MISURE, Note di indirizzo sviluppate dalla Rete dei Laboratori delle Agenzie per l’Ambiente, N. 1/TTA/09
[7] Incertezza di misura, Da Wikipedia, l’enciclopedia libera
[8] International Organization for Standardization. Guide to the expression of uncertainty in measurement. Geneva: ISO, 1993. Nuova edizione corretta nel 1995.
[9] UNI CEI ENV 13005 “Guida all’espressione dell’incertezza di misura”, 2000, Milano,
[10] La nuova Guida di riferimento per l’espressione dell’incertezza di misura, Accredia, 07 gennaio 2016
[11] Università La Sapienza di Roma, Incertezza di misura, capitolo 15, Impatto ambientale dei campi elettromagnetici
[12] UNI CEI 70098-3 Incertezza di misura – Parte 3: guida all’espressione dell’incertezza di misura, settembre 2016
[13] La validazione dei metodi ed incertezza di misura nei laboratori di prova: le linee guida delle Agenzie Ambientali, Ancona 2003, Guida all’espressione dell’incertezza di misura, S.
Aggiornamento del 22 agosto 2020
autore: Marco Morelli

